Die Kaprekar Konstante 6174
a) Zahlensummen
1 Erloschener externer Link ist grau unterlegt.
a) Zahlensummen
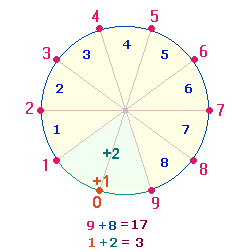
1. Dem indische Mathematiker KAPREKAR (1905-1986) ist die sogenannte Kaprekar Konstante zu verdanken. Wenn man die Ziffern z.B. einer vierstellige Zahl, die nicht alle gleich sind, einmal von oben nach unten und einmal umgekehrt anordnet, die Differenz zwischen beiden ermittelt und dasselbe Verfahren wiederholt, gelangt man nach spätestens 7 Durchgängen zur Endzahl 6174, da 7641-1467 wiederum 6174 ergibt. Eine solche Konstante gibt es auch für dreistellige Zahlen (495) und für 6- und 9-stellige Zahlen.
2. Für diese Konstanten gibt es wissenschaftliche Beweisverfahren. Ich beschränke mich auf eine eher deskriptive Betrachtung. Ausgangspunkt ist die rationale GEGEBENHEIT des regelmäßigen Zahlenpaares 4321-1234 = 1029 = 3*7³. Wenn man die vier Ziffern, von der obersten angefangen, als abcd bezeichnet, erhält man folgende Gleichung:
1000a+100b+10c+d
– 1000d-100c-10b-a =
999a+90b-90c-999d
=
999(a-d)+90(b-c)
=
9*[111*(a-d) + 10*(b-c)]
Auf die beiden Modellzahlen angewendet lautet die Rechnung
9*[111*(4-1) + 10*(3-2)] =
9*(111*3 + 10*1) =
9*(333 + 10) = 9*343 = 3087
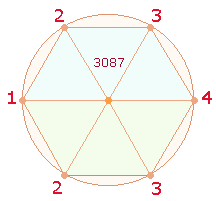
3087 ist die Hälfte von 6174, was bedeutet, daß diese Zahl erreicht wird, wenn a-d = 6 und b-c = 2. Dies ist der Fall bei Verdoppelung von 4321 zu 8642 und einer Reihe anderer Zahlen, z.B. 8752, 9753, 9643, 7531, 7421, 7311 usw.
Die folgende Rechnung als Fortsetzung des Grundmodells ist:
8730-0378 = 9*(111*8 + 10*4) = 9*(888 + 40) = 9*928 = 8352
Der dritte Durchgang führt zur Endzahl 6174:
8532-2358 = 9*(111*6 + 10*2) = 9*(666 + 20) = 9*686 = 9*2*343 = 6174
Die von 6174 zu 7614 umgestellte Zahl erfüllt die Bedingung von a-d = 6 und b-c = 2 und führt daher zur Zahl 6174 zurück.
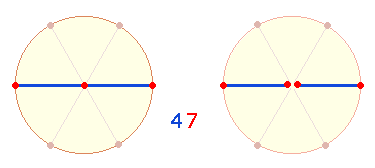
3. Zwei linear fortschreitende vierstellige Umkehrzahlen sind stets durch 1111 = 11*101 teilbar. Multiplikationsfaktor ist die Quersumme einer Zahl durch 2: 1234+4321 = 5555 = 5*1111.
Bei den hier verwendeten Beispielen sind jeweils zwei Umkehrpaare durch 1111 teilbar:
|
B1 |
sm |
|
B2 |
sm |
|
||
|
8730 |
8532 |
17262 |
18*959 |
8532 |
7641 |
16173 |
9*1797 |
|
378 |
2358 |
2736 |
18*152 |
2358 |
1467 |
3825 |
9*425 |
|
9108 |
10890 |
19998 |
18*1111 |
10890 |
9108 |
19998 |
9*2222 |
Die Summen 10890 und 9108 in beiden Beispielen erweisen sich als Umkehrzahlen 1210 = 110*11 und 1012 = 92*11, wenn man sie durch 9 teilt. Die Umkehrung besteht in der Umstellung der Zahlen 12 und 10. Auf ihre Bedeutung wird weiter unten eingegangen.
4. Welches Gesetz jede beliebige vierstellige Zahl notwendigerweise zu 6174 führt,
habe ich nicht gefunden. Es scheint mir daher nützlich, die einzelnen Schritte
eines solchen Vorgangs zu verfolgen. Ich nehme die Zahl 5321:
|
|
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
|
5321 |
8640 |
8721 |
7443 |
9963 |
6642 |
7641 |
49050 |
|
|
1235 |
0468 |
1278 |
3447 |
3699 |
2466 |
1467 |
12825 |
|
sm |
|
9108 |
9999 |
10890 |
13662 |
9108 |
9108 |
61875 |
|
/9 |
|
1012 |
1111 |
1210 |
27*506 |
1012 |
1012 |
|
|
a-d b-c |
4 1 |
8 2 |
7 5 |
4 0 |
6 3 |
4 2 |
6 2 |
|
|
*9 |
454 |
908 |
|
444 |
696 |
464 |
686 |
|
|
sm |
4086 |
8172 |
7443 |
3996 |
6264 |
4176 |
6174 |
36225 |
|
|
2*227 |
4*227 |
827 |
12*37 |
24*29 |
16*29 |
2*7³ |
|
|
12825:49050 = 15²*(19:2*109) = 225*275 = 15²*15*(9*11) |
||||||||
|
36225 = 15²*7*23 |
||||||||
Die Ausgangszahl 5321 gelangt durch weitere 6 Zahlen zur Konstante 6174. Diese 6 durch 9 teilbare Zahlen sind jeweils für die nächste Zahl Wegbereiter für das Endresultat. Dazu gibt es eine vollständige Übersicht am Ende einer Website. Es finden sich dort alle Varianten der Subtraktionen a-d und b-c:
|
1 |
1 |
7641 |
|
|
|
|
|
|
|
|
|
|
|
7641 |
|
2 |
3 |
4176 |
8352 |
8532 |
|
|
|
|
|
|
|
|
|
21060 |
|
3 |
12 |
6264 |
3087 |
4266 |
2088 |
7083 |
7353 |
7533 |
8082 |
9171 |
9261 |
9711 |
9621 |
83520 |
|
4 |
9 |
3996 |
1998 |
1089 |
4356 |
6354 |
6993 |
8991 |
9081 |
9801 |
|
|
|
52659 |
|
5 |
10 |
7443 |
3177 |
5265 |
5355 |
5445 |
6444 |
7173 |
6660 |
8262 |
8622 |
|
|
63846 |
|
6 |
11 |
8172 |
2997 |
3267 |
4995 |
5994 |
7263 |
7623 |
7992 |
2178 |
8712 |
7992 |
|
67185 |
|
7 |
8 |
4086 |
5085 |
5175 |
6084 |
8442 |
9351 |
9441 |
9531 |
|
|
|
|
57195 |
|
|
54 |
4 1 |
345465 = 34*5*853; 353106 = 54*13*503 = 54*6539 |
345465 |
||||||||||
Die linke Spalte enthält die dem Muster 4 1 zugehörigen Zahlen. Die Gesamtsumme 345465 berücksichtigt nur die hinführenden Zahlen. Durch Hinzufügung von 7641 ergibt sich der Durchschnittswert 6539 für 54 Zahlen. Eigentlich würde man das Subtraktionsergebnis 6174 statt 7641 erwarten. Diese Summe ist 351639 = 3²*89*439.
5. Einer anderen Website entnehme ich die Anzahl der Zahlen und der Stufen, die zu 6174 führen:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
1 |
357 |
519 |
2124 |
1124 |
1379 |
1508 |
1980 |
8991 |
Die vom Verfasser unter 0 angegebene Zahl 1 soll wohl 7641 bedeuten. Sie ist aber nicht anders zu behandeln als die 356 anderen. Die hohe Zahl 357 des Sofortergebnisses von 6174 ist bedingt durch 24 Umkehrungen jeder Zahl. Die Zahl der Umkehrungen reduziert sich durch Doppelzahlen und durch die Null. Es handelt sich um nicht mehr als 20 Ausgangszahlen:
|
9973 |
8862 |
7751 |
12 |
6640 |
9 |
|
9863 |
8752 |
7641 |
24 |
6530 |
18 |
|
9753 |
8642 |
7531 |
24 |
6420 |
18 |
|
9643 |
8532 |
7421 |
24 |
6310 |
18 |
|
9533 |
8422 |
7311 |
12 |
6200 |
6 |
|
|
|
|
96 |
|
69 |
|
3*96+69 = 357 |
|||||
Die Quersumme aller 20 Zahlen ist 360, im Durchschnitt 18. Die Quersumme 18 haben nur 8532 und 7641. Sie stehen konzentrisch in 9. und 12. Position, ihre Summe und Umkehrsumme beträgt daher jeweils ein Zehntel der Gesamtsumme 180*1111: 16173 =3³*599; 3825 = 3²*5²*17 = 25*153; 16173+3825 = 19998 = 18*1111. Die Summe 3825 ist eine der Umkehrungen von 8532.
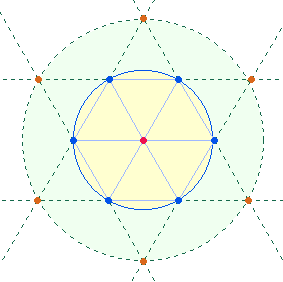
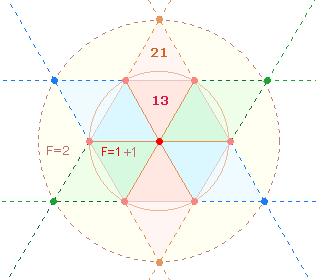
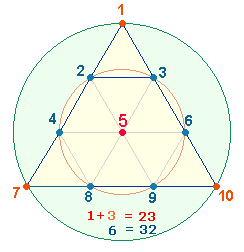
6. Es gibt kaum eine Zahl, die man nicht auf das HEXAGRAMM, auch Tetraktysstern genannt, beziehen könnte. Dieses entsteht durch Verlängerung der Segmentlinien eines Hexagons:
|
|
Die Zahl 6174 weist auf diese Entfaltung hin: Das Hexagon besteht aus 6 Kreislinienpunkten und dem Mittelpunkt, eine Tetraktys aus 10 Punkten, 18 Linien und 9 Dreiecken, zusammen aus 37 Elementen, die verdoppelt 74 ergeben.
Die mit 9 zu multiplizierende Ausgangssumme war 343 = 7³. Die Zahl 343 selbst weist auf die 3 Tetraktysseiten hin, von denen jede aus 4 Punkten und 3 Linien besteht:
|
|
Die Verdoppelung der Summe 343 entspricht zwei Tetraktys. Der Faktor 2 kann jedoch auch zum Multiplikator 9 hinzugenommen werden. Dann besteht die Aufteilung der drei Tetraktysseiten in 9 Punkten und 9 Linien:
|
|
7. Die Beziehung der Kaprekar Konstante 6174 zur Tetraktys liegt nahe, da ja die Tetraktys ein Zahlendreieck von 4 Punkteebenen darstellt, deren Summe 10 konstitutiv für das Dezimalsystem ist.
Der Faktorenwert (FW), d.h. die Summe der Faktoren, der Zahl 6174 ist 2*3²*7³ = 29, der FW der Zahl 8352 3²*25*29 = FW 45. Die Zahlen 29 und 45 sind mehrfach verknüpft:
|
|
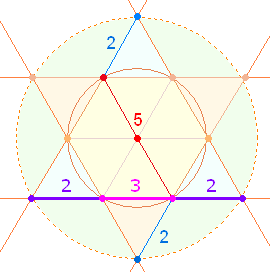
Der Zickzackdurchmesser besteht aus 9 Elementen, 2+2 Erweiterungs- und 5 hexagonalen Elementen. Die Summe der Zahlen von 1-9 ist 45, numeriert man jedoch den Durchmesser vom Mittelpunkt aus von 1-5, ist die Summe 29.
Der zusammengesetzten Zahl 252 des Durchmessers entspricht die Palindromzahl 232 einer Tetraktysseite mit den Faktoren 2³*29. In der Zahl 928 des zweiten Durchgangs ist 232 viermal enthalten.
Bemerkenswert ist, daß der Faktor 29 in der Zahl 4321 selbst enthalten ist: 29*149. Die Zahl 149 gibt die 9 aufaddierten Dreiecke der Tetraktys wieder.
8. Was bei der Ermittlung der Kaprekar Konstante als Subtraktionsvorgänge erscheint, sind in Wirklichkeit eine Zahlenumkehrungen, die in kreisförmiger Weise zur Ausgangszahl zurückführt:
|
|
Die Umkehrzahl schließt den Kreis und schafft als Inhalt und Bedeutung die Differenz zwischen 1234 und 4321. Die Differenz 3087 weist über das Hexagon hinaus auf seine Weiterentfaltung zum Tetraktysstern.
b) Zahlen- und Faktorensummen
1. Bereits im vorangegangenen Abschnitt traten die Faktoren der Zahl 6174 in Erscheinung. Nun geht es darum, Zahlensummen (ZS) und Faktorensummen (FS) miteinander zu verrechnen. Zu untersuchen und zu verrechnen sind die Zahlen 1467, 6174 und 7641.
Die Faktoren der Zahl 1467 sind 3²*163 = FW 169 = 13². Die Primzahl 163 gibt die Punktestruktur der Tetraktys wieder: Mittelpunkt, 6 Kreislinienpunkte, 3 Eckpunkte.
Die Faktoren der Zahl 7641 sind 3³*283 = FW 292 = 4*73.
2. Die ZW/FW-Verrechnung
ergibt:
|
|
|
|
sm |
FW |
sm |
FW |
|
Zahl |
1467 |
6174 |
7641 |
292 |
|
|
|
FW |
169 |
29 |
198 |
19 |
|
|
|
sm |
3³*13*67 |
7839 |
311 |
8150 |
175 |
|
|
FW |
|
|
86 |
311 |
397 |
397 |
|
8150 = 50*163 |
572 |
|||||
|
572 = 4*11*13 >FW 28 |
||||||
Der Faktor 163 tritt in der Zahl 8150 ein zweites Mal in Erscheinung. Die Zahl 50 ist als 2*25 Elemente des Hexagons und der Erweiterung zu verstehen, wenn zur Kreisziehung des äußeren Tetraktyskreises der hexagonale Mittelpunkt ein zweites Mal verwendet wird.
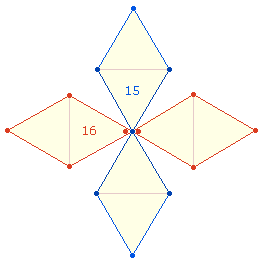
3. Die Faktoren 11 und 13 der Zahl 572 sind als Elemente zweier geometrischer Figuren zu verstehen, die zur Bildung eines Oktaeders führen:
|
|
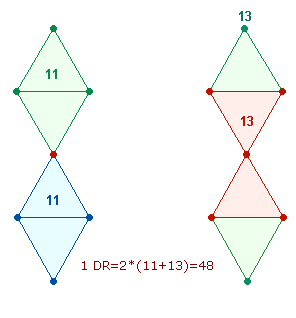
Im Hexagramm sind drei Doppelrauten (DR) zu erkennen. Aus einem Doppeldreieck des Hexagons entstehen durch dessen Erweiterung zum Tetraktysstern zwei Rautenfiguren. Aus einem Achsenkreuz zweier Doppelrauten läßt sich ein Oktaeder zusammenfügen. Wenn die beiden äußeren Punkte vereinigt werden, entsteht ein zweites Doppeldreieck aus 13 Elementen.
Je nachdem, von welcher Perspektive man einen Oktaeder betrachtet, besteht er entweder aus 4 Doppeldreiecken oder 4 Doppelrauten, oder aus 2 Doppeldreiecken und 2 Doppelrauten. Dies ist die Bedeutung des Faktors 4.
Bemerkenswert sind 22+26 als ZS der Initialen IN-RI und der Buchstabenzahlen der historischen und der biblischen Kreuzesinschrift.
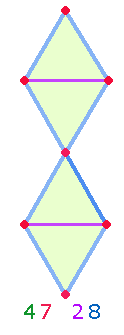
4. Die Zahl 28 als FW der Zahl 572 ist ein Merkmal der DR. Denn die Rechnung 28 = 7*4 enthält die 4 Ziffern, die die 21 Elemente der DR ausmachen: 8 Rahmenlinien und 2 Querlinien, 7 Punkte und 4 Dreiecke:
|
|
28 Elemente entsprechen auch 4 Dreiecken, da ein einzelnes aus 7 Elementen besteht, in der DR sind die Elemente jedoch auf 21 verkürzt.
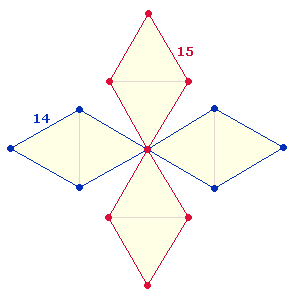
5. Die DR führt zu einer weiteren Bedeutung der Einzelziffern der Kaprekar Konstante 6174: Die DR besteht aus 6+1 Punkten, ein Dreieck aus 7 Elementen. Durch die Erweiterung kommen 4 Elemente hinzu, die die Rautenfigur konstituieren.
Die Aufteilung von Punkten und Elementen hat Bedeutung hinsichtlich der Kreisflächenverhältnisse der beiden Tetraktyskreise: Der Erweiterungsring des äußeren Kreises hat die doppelte Fläche des hexagonalen Kreises, d.h., das Verhältnis des äußeren zum inneren Kreis beträgt 3:1:
|
|
Nun umfassen 6 DR-Punkte den ganzen äußeren Kreis, also den Erweiterungsring und das Hexagon, repräsentieren also 3 Flächeneinheiten, der Mittelpunkt jedoch nur den hexagonalen Kreis mit 1 Flächeneinheit. Die 7 Elemente des hexagonalen Dreiecks geben 1 Flächeneinheit wieder, die 4 Erweiterungselemente 2 Flächeneinheiten. Die Flächenentsprechungen der 4 Einzelziffern sind demnach:
|
6 |
1 |
7 |
4 |
|
3 |
1 |
1 |
2 |
|
11 |
14 |
||
Die Summen 11+14 = 15 stellen zwei Aspekte der Raute dar: 11 tatsächliche Elemente und 14 Elemente, wenn man für jedes Dreieck 7 zählt.
6. Eine Fläche ist der Inhalt einer durch Punkte und Linien bewirkte Begrenzung, die man als Rahmen bezeichnen kann. Beide stehen in Wechselbeziehung zueinander. Der Rahmen eines DR-Kreuzes besteht aus 29 Punkten bei einem und aus 31 Punkten bei drei Mittelpunkten:
|
|
|
Die komplementäre Zahl von 1:3 Mittelpunkten und 29 und 31 Rahmenelementen gewährleistet, daß jeder DR-Rahmen seine 15 Elemente bewahrt.
Der Faktor 283 der Zahl 7641 ist zu verstehen als 28 Rahmenelemente mit 3 Mittelpunkten.
7. Die Zahlen 1 und 3 bilden den Ausgangspunkt und die Rückkehr aller Zahlen. Sie haben trinitarische Bedeutung, d.h., sie sind Abbild des einen Gottes in drei Personen. Die beiden Zahlen zeigen sich in der eingangs entwickelten Formel, in der 4-1 und 3-2 zu 3 und 1 reduziert werden. Die umgekehrte Ausweitung des Verhältnisses 3:1 zeigt sich in der Teilung der Kreislinie:
|
|
Durch die Teilung des Kreisbogens wird jede Hälfte durch 1 Bogenhälfte und 2 Punkte bezeichnet, beide Hälften aber bestehen aus 4 Elementen. Auf diese Weise wird aus 3:1 die Summe 10.
8. Die beiden trinitarischen Verhältnisse 1:3 und 1:2 sind auch als zusammengesetzte Zahlen 13+12 von Bedeutung:
·
Das Hexagon
besteht aus 25 Elementen: aus 7 Punkten + 6
Dreiecken und 6+6 Linien.
·
Das Grundquadrat mit
Mittelpunkt besteht aus 9
Punkten + 4 Einzelquadraten und 12 Linien.
·
Im Tetraktysstern werden Punkte
und Dreiecke zu 13+12 erweitert.
Die Einzelziffern der Zahl 25 weisen auf 2 Erweiterungs- und 5 hexagonale Punkte der DR hin, sie geben das Kreisflächenverhältnis 2:1 wieder.
Für die beiden
zweistelligen Zahlen und ihre Umkehrungen ergeben sich folgende ZS+FS:
|
|
|
|
sm |
|
|
sm |
GS |
|
ZW |
12 |
13 |
25 |
21 |
31 |
52 |
77 |
|
FW |
7 |
13 |
20 |
10 |
31 |
41 |
61 |
|
|
20 |
26 |
45 |
31 |
62 |
93 |
138 |
|
20:25 = 5*(4:5); 93 = 3*31 |
|||||||
Die Zahl 325 ist die Summe der Zahlen 1-25, ihre Einzelziffern weisen auf die bereits gezeigten Radialelemente und durch 4+5 bzw. 9*5 auch auf die Durchmesserelemente der DR-Zickzacklinie hin. Die entsprechende FS ist 220. Die ZS+FS 545 spiegelt das FS:ZS-Verhältnis 5*(4:5) wider.
Die FS 61 – als Bestandteil der Konstante 6174 – und die ZS+FS 93 = 3*31 lassen sich auf die 7 Punkte der DR beziehen.
9. Einen Hinweis auf die Zahlen 12 und 13 gibt die Summe der Teiler der Kaprekar Konstante 6174. Sie beträgt 15600 = 12*13*10*10 = FW 34. Die Quadratzahl von 10 läßt sich auf die Punkte von zwei Tetraktys beziehen. Der Durchschnittswert der 24 Teiler ist 650, was durch 13*50 wiederum den FW 13+12 = 25 ergibt. Der FW 34 kann als 13:21 Elemente der Doppelraute gelesen werden, die das Kreisflächenverhältnis 1:3 wiedergeben:
|
|
Die Summe der 12 unteren Teiler ist 235 = 5*47, die der oberen 15365 = 5*7*439. Das Hexagon und die hexagonale Erweiterung bestehen jeweils aus 12 Linien bzw. Maßeinheiten.
c) 10 Maßeinheiten und
ihre Begrenzungen
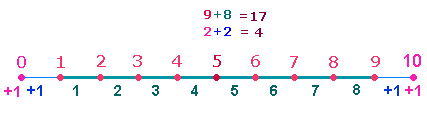
1. Geht man vom Kreis als Urmodell alles Zählbaren aus, so tritt das Maß des Radius durch Erstellung einer Kreisachse als zwei LINIEN in Erscheinung. Sie werden jeweils durch zwei Punkte begrenzt. Man muß also den Mittelpunkt zweimal zählen. In der Kombination von einem und zwei Mittelpunkten erhält man 7 Punkte und 4 Linien bzw. Maßeinheiten:
|
|
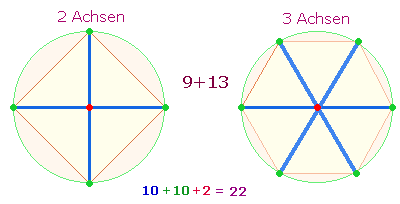
2. Eingangs wurden die beiden Umkehrsummen 1210 und 1012 ermittelt. Sie stellen 10 Maßeinheiten dar, die durch 12 Punkte in zwei geometrischen Achsenfiguren begrenzt werden:
|
|
Die Bedeutung der Zahlen 1210 und 1012 erhellt sich weiter, wenn man sie durch 22 teilt: 55 ist die ZS, 46 die FS der Zahlen 1-10. Die FW der beiden Zahlen sind die Quadratzahlen 16 und 25 und bewirken, daß die Summe jeweils 71 beträgt. Die Komplementärzahl zu 71 ist 39, deren Faktoren 3*13 als Einzelziffern die 7 Punkte der DR wiedergeben. Die Einzelziffern der Zahl 71 bedeuten entweder die Rahmenelemente einer Raute mit der 1 als Mittelpunkt einer DR oder 7 Punkte der DR und ein zweiter Mittelpunkt.
Die Einzelziffern der 9+13 Elemente spiegeln die Punkteaufteilung des Tetraktyssterns wider. Sie sind daher auch in den dreistelligen Zahlen 913 = 83*11 und 139 sowie im Produkt 13*9 = 117 vertreten.
1. Aufgrund der bisherigen Überlegungen sind die einzigen zwei durch 18 teilbaren Zahlen 8532 und 7641 mit ihren Umkehrungen als komplementär anzusehen. Hinsichtlich der Grundlagen des Dezimalsystems ist von ihnen also einige Auskunft zu erwarten. Eine Möglichkeit, sie in Beziehung zueinander zu setzen, ist, jede Zahl in zwei zweistellige Zahlen aufzuteilen und sowohl ZS als auch FS zu ermitteln.
Die Elemente 13+9 der beiden Achsenfiguren sind in der jeweiligen Ausgangszahl und in ihrer Umkehrung zweifach zu erkennen: 85+32 bzw. 76+41 = 117 = 13*9. 23+58 bzw. 14+67 = 81. 117:81 = 9*(13:9). Der FW der Umkehrung 2358 = 2*3²*131 >139.
2. Die Aufteilung 61+74 der Konstante 6174 führt zur ZS 135 und FS 61+39 = 100. Das FS:ZS-Verhältnis 5*(20:27) = 5*47 weist wiederum auf die Elemente der beiden Achsenfiguren hin. Die ZS 27 setzt sich zusammen aus dem Doppelaspekt von 10+2 und 10+5 Punkten. 2+3 Punkte ergeben sich aus einem Mittelpunkt je Achse.
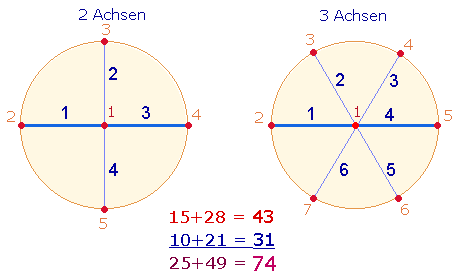
3. Punkte und Linien der beiden Achsenkreuze können auch numeriert werden:
|
|
Die
Zusammenlegung von unnumerierter und numerierter Zählweise ergibt:
|
|
numer. |
|
unnum. |
|
|
||
|
|
3 A. |
2 A. |
sm |
3 A. |
2 A. |
sm |
GS |
|
Pu. |
28 |
15 |
43 |
7 |
5 |
12 |
55 |
|
Li. |
21 |
10 |
31 |
6 |
4 |
10 |
41 |
|
|
49 |
25 |
74 |
13 |
9 |
22 |
96 |
Die Summen 12 und 43 könnten eine Erklärung für Vergils 9896 Verse der Aeneis sein. Denn die Faktoren 2³*1237 führen zum FW 1243.
Die aufgezeigten
Ergebnisse lassen sich in den FS der
aufgeteilten Ausgangszahlen 8532 und 7641 erkennen:
|
|
|
|
sm |
|
|
sm |
GS |
|
ZW |
85 |
32 |
117 |
76 |
41 |
117 |
|
|
FW |
22 |
10 |
32 |
23 |
41 |
64 |
96 |
|
|
|
|
149 |
|
|
181 |
|
|
32:64 = 32*(1:2) |
|||||||
Die Summe 96 ist deswegen besonders bedeutsam, weil die FW 10 und 12 der FS 32 und 64 die Zahl der unnumerierten Linien und Punkte ergeben.
4. Ein weiteres Problem der 10 Maßeinheiten besteht darin, daß die Grundzahlen 1-9 nur 8 Maßeinheiten begrenzen. Sie werden erst vollständig durch Hinzunahme der 0 und der 10:
|
|
Kennzahlen für 10 Maßeinheiten und 11 Punkte sind daher 28, 29, 181, 191, 174, 417. Setzt man die Null in die Mitte eines Kreises, entfällt ein Punkt, 2-stellige Kennzahlen sind daher und 19 91 173, 317.
|
|
Dreistellige Kennzahlen finden sich in den FS der Zahlen 8532 und 7641 und ihren Umkehrungen:
|
92 |
2358 = 2* 3²* 131 |
139 |
231 |
|
|
7641 = 3³* 283 |
292 |
1467 = 3²* 163 |
169 |
461 |
|
16173 |
|
3825 |
|
|
|
22+362 |
384 |
14+294 |
308 |
692 |
|
362 =2*181; 294 = 2*3*7²; 692 = 4*173 = FW 177 |
||||
|
384:308 = 4*(96:77) = FW
8+(13+18)=8+31= 3*13 = 16 |
||||
Die FS setzt sich aus 3+10 Faktoren der Zahlen 2 und 3 und aus 4 höheren Primzahlen, also aus 17 Faktoren, zusammen. Bei Trennung der beiden FS ergibt sich 36+656 = 4*(9:164) = 4*173.
294 ist die FS der Zahlen 1-30. 10 Maßeinheiten können durch je 2 Zahlen begrenzt werden, z.B. 1-2-3, 4-5-6 usw. Siehe dazu eine detaillierte Untersuchung.
Die ZW/FW-Verrechnung der FS 384 und 308 ergibt 177+16 = 193. Die Einzelziffern der Primzahl 193 geben die Punkteaufteilung des Tetraktyssterns wieder.
5. Zwei dreistellige Kennzahlen des Dezimalsystems erscheinen auch, wenn die ZS+FS der zweistelligen Aufteilungen der Zahlen 7641, 8532 mit ihren Umkehrungen und zweimal der Konstante 6174 ermittelt werden:
|
76 |
41 |
14 |
67 |
61 |
74 |
333 |
85 |
32 |
23 |
58 |
61 |
74 |
333 |
|
23 |
41 |
9 |
67 |
61 |
39 |
240 |
22 |
10 |
23 |
31 |
61 |
39 |
186 |
|
|
|
|
|
|
|
573 |
|
|
|
|
|
|
519 |
|
573:519 = 3*(191:173) = 1092; 191+173 = 364 |
|||||||||||||
Die Einzelziffern der Summe 364 teilen die 13 Punkte des Hexagramms auf in 6 Kreislinienpunkte, 1 Mittelpunkt + 3 Eckpunkte einer Tetraktys und 3 weitere Eckpunkte. Die Zahl von 4+6 Punkten, die den Maßeinheiten der beiden Achsenkreuze entsprechen, haben in der numerierten Tetraktys die Umkehrsummen 23+32 = 55:
|
|
Die Summe 55 ergibt sich aus der Zahl 1092, wenn man sie mit den zwei ZS und FS verrechnet:
|
|
ZS |
FS |
ZS |
FS |
sm |
FW |
|
|
333 |
240 |
333 |
186 |
1092 |
27 |
|
FW |
43 |
16 |
43 |
36 |
138 |
28 |
|
sm |
|
|
|
|
|
55 |
6. Je komplexere Zahlenzusammenhänge untersucht werden, umso schwieriger ist ihre Auswertung und Deutung. Entscheidend ist die Wahl der richtigen Ordnungsstrukturen, in deren Rahmen Inhalte ihren Sinnzusammenhang zu erkennen geben. Im vorliegenden Fall wird angenommen, daß die ZS und FS der vier- und zweistelligen Zahlen eine Einheit bilden. Weitere Grundlage ist die Gleichung 1+2=3, d.h. der größeren Zahl werden die Umkehrzahl und ihr Subtraktionsergebnis gegenübergestellt. Da es sich um zwei komplementäre Zahlen handelt, ergibt sich somit ein Quadrat von vier Feldern, denen die vier Punkteebenen der Tetraktys entsprechen.
|
8532 |
85 |
32 |
|
|
|
8649 |
92 |
22 |
10 |
|
|
|
124 |
|
7641 |
76 |
41 |
|
|
|
7758 |
292 |
23 |
41 |
|
|
|
356 |
|
|
|
|
|
|
|
16407 |
|
|
|
|
|
|
480 |
|
2358 |
23 |
58 |
6174 |
61 |
74 |
8748 |
139 |
23 |
31 |
29 |
61 |
39 |
322 |
|
1467 |
14 |
67 |
6174 |
61 |
74 |
7857 |
169 |
9 |
67 |
29 |
61 |
39 |
374 |
|
|
|
|
|
|
|
16605 |
|
|
|
|
|
|
696 |
Das Verhältnis der FS 480:696 ist 24*(20:29) = 1176. Die Summe 16407+16605 = 33012 ist darstellbar als Palindromprodukt 252*131. Da 252 aus dem Umkehrprodukt 12*21 besteht, sind im Ergebnis die beiden Kreisflächenverhältnisse 1:2 und 1:3 vertreten.
Die Faktoren der ZS+FS 33012+1176 = 34188 sind 3*4*7*11*37 = FW 62. Das Ergebnis gibt Auskunft über die Bedeutung der Zahl 62, deren Einzelziffern für das Zustandekommen der Kaprekar Konstante wesentlich sind. Der FW 62 setzt sich zusammen aus 25+37: Die 25 Elemente Hexagon und 37 Elemente der Tetraktys vertreten das Kreisflächenverhältnis 1:3 der beiden konzentrischen Tetraktyskreise.
Die Einzelziffern 6 und 2 können als 3+1/1+3 auf die 7 Punkte der DR bezogen werden, wenn für jede Raute ein eigener Mittelpunkt gezählt wird:
|
|
Die Zahl 26 ist
bedeutsam wegen der 26 Elemente des Oktaeders und des Würfels.
Erstellt: September 2015