Trinitarische Bedeutung der Zahlen 13
und 31
a) Einleitung
b) 13 bis 31 auf dem Tetraktysrahmen
c) 13 bis 31 auf Punkten und in Dreiecken
d) 13-31 und 12-21; Vertiefung
a) Einleitung
1. Im Buch der Weisheit 11, 20 preist der Verfasser Gott mit den Worten: "Du hast alles nach Maß, Zahl und Gewicht geordnet." Wenn nun die Schöpfung eine innere Ordnung als ganze, in jedem Einzelnen und in der Beziehung von allem zueinander besitzt, dann trifft dies umso mehr auf die Zahlen selbst zu. Voraussetzung hierfür ist, daß das Dezimalsystem dem göttlichen Ordnungssystem entspricht, also auf keine rein menschliche Festlegung beruht.
Nun ist Gott ein einziger, jedoch in der Gemeinschaft dreier Personen. Dieser Gott in drei Personen ist in seiner Vollkommenheit alternativlos, und ebenso alles Geschaffene und Erkennbare. Denn es ist nicht denkbar, daß der vollkommene Gott etwas schafft, das außerhalb seiner selbst eine Ordnung darstellt. Daher ist auch die vollkommene Ordnung der Zahlen Abbild der unübertreffliche Weisheit des dreieinen Gottes.
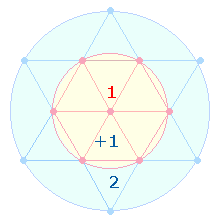
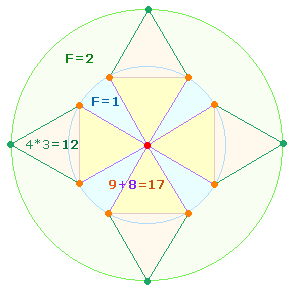
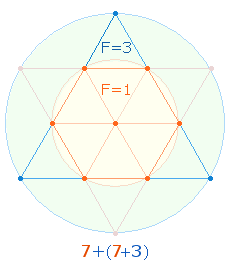
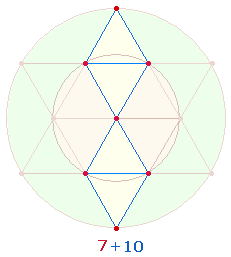
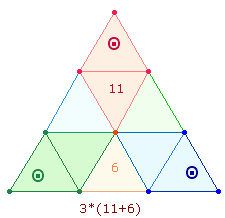
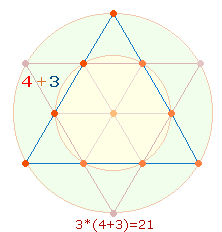
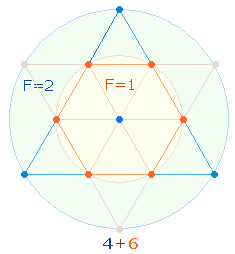
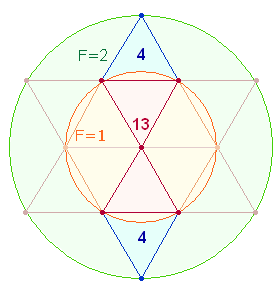
Wesentliches Zeugnis für die apriorische Geltung des Dezimalsystems ist das Hexagramm (Tetraktysstern), dessen zwei konzentrische Kreise das Kreisflächenverhältnis 1:3 bzw. 3:1 besitzen. Im Hexagramm sind zwei gleichseitige Zahlendreiecke (Tetraktys) von jeweils 10 (1-4) Punkten enthalten, die 18 Linien und 9 Binnendreiecke begrenzen:
|
|
Der Tetraktysstern selbst besteht aus 13 Punkten, Hinweis darauf, daß die Zahlen 13 (und 31) die Natur des dreieinen Gottes am angemessensten wiedergeben.
2. Es gibt zwei duale Zahleneinteilungen:
·
in ungerade und gerade Zahlen
·
in Zahlen aus einem Faktor, Primzahlen genannt,
und Zahlen, die aus mehreren Faktoren multiplikativ zusammengesetzt sind. Die
Zahl 1 scheidet als Faktor aus, da sie
lediglich eine Zahl initial als multiplikativ erweiterbar bezeichnet, die Zahl
selbst aber nicht verändert.
Wenn die Zahlen eine innere SINNSTRUKTUR
besitzen, dann muß in den beiden dualen Einteilungen eine sinnvolle Ordnung
enthalten sein. Sie kann nicht anders als darin bestehen, daß die Faktoren von fortlaufenden Zahlen oder von
Zahlengruppen addiert werden und mit den Summen der Zahlen selbst in Beziehung
gesetzt werden. Als Beispiel seien die Zahlen von 1-21
angeführt: Die Faktorensumme
(FS) 165 und die Zahlensumme (ZS)
231 sind durch 33 teilbar und haben
das Verhältnis 5:7. Die 9 Primzahlen und die 12
übrigen Zahlen haben in Umkehrform das FS-Verhältnis
78:87, das auf die Rahmenelemente der Doppelraute
(DR) von 7
Punkten und 8 Linien hinweist.
In richtiger Betrachtungsweise hat jedes Ergebnis Bedeutung. Das Erfordernis für das Wesentliche bedingt eine sehr eingeschränkte Berücksichtigung der vielen Einzelergebnisse.
b)
13 bis 31 auf dem Tetraktysrahmen
1. Von der Zahl 13 bis einschließlich 31 sind es 19 Zahlen. Es ergeben sich folgende ZS und FS:
|
Z.folge |
13 |
14 |
15 |
16 |
17 |
75 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
198 |
27 |
28 |
29 |
30 |
31 |
145 |
418 |
|
FW |
13 |
9 |
8 |
8 |
17 |
55 |
8 |
19 |
9 |
10 |
13 |
23 |
9 |
10 |
15 |
116 |
9 |
11 |
29 |
10 |
31 |
90 |
261 |
|
|
|
|
|
|
|
130 |
|
|
|
|
|
|
|
|
|
314 |
|
|
|
|
|
235 |
679 |
|
55+90 = 145; 145:116 =
29*(5:4) = 9*29;
679 = 7*97 >FW 104 = 8*13 |
|||||||||||||||||||||||
In konzentrischer Zählung ist das FS-Verhältnis von
10:9 Zahlen 29*(5:4).
Der Primfaktor 97 der
Gesamtsumme ist die letzte zweistellige Umkehrzahl und Komplementärzahl zu 13.
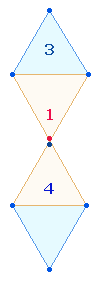
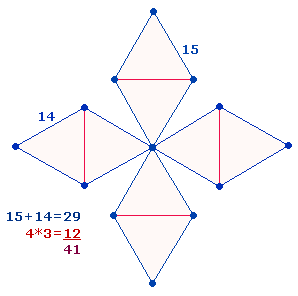
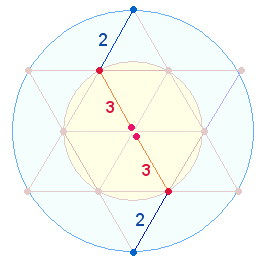
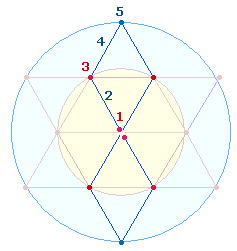
Der durchschnittliche Zahlenwert (ZW) der 19 Zahlen ist 22. Er verweist auf die Elemente von zwei miteinander verbundenen Rauten zur Doppelraute (DR) bei je einem Mittelpunkt. Im Tetraktysstern sind drei Doppelrauten zu erkennen. Die Einzelziffern der Primzahlen 31 und 13 geben die Punktestruktur der DR wieder und können als Gleichung 3+1 = 4 wiedergegeben werden:
|
|
In dreistelliger Zusammensetzung ist 314 die ZS+FS der mittleren 9 Zahlen 18-26.
2. Die Summe der übrigen vier Primzahlen 17+19+23+29 ist 88 und analog zu 13+31 auf die zwei anderen DR des Tetraktyssterns beziehbar. Es ergibt sich also das Verhältnis 22*(6:13) der Primzahlen zu den zusammengesetzten Zahlen. Die Einzelziffern des Verhältnisses bezeichnen die Struktur der 10 Tetraktyspunkte: 6 Kreislinienpunkte, Mittelpunkt + 3 Eckpunkte.
3. Über die Faktoren 9*29 der FS 261 ist folgendes zu sagen:
Die DR-Zickzacklinie besteht aus 5 Punkten + 4 Linien, also aus 9 Elementen, die als Numerierungssumme vom Mittelpunkt aus 29 ergeben. Die Einzelziffern der FS 261 weisen auf 9 Punkte des Tetraktysrahmens hin. Eine Tetraktysseite besteht aus 2+3+2 Elementen, 3 gehören zum Hexagon, 2+2 zum Erweiterungsbereich. Die dreistellige Zahl 232 hat die Teiler 8*29.
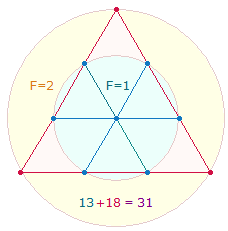
Die drei Tetraktysseiten aus 18 Elementen schließen die drei Hexagonachsen aus 13 Elementen, sodaß 13+18 die Umkehrzahl 31 ergibt:
|
|
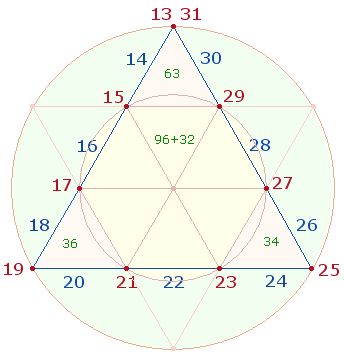
4. Es liegt nahe, die 19 Zahlen so auf den Tetraktysrahmen anzuordnen, daß die beiden Umkehrzahlen 13 und 31 nebeneinander stehen:
|
|
Ein FS+ZS-Verhältnis ist nicht zu finden. Von Interesse sind die FS der 3*3
hexagonalen Elemente und 4+3+3
Erweiterungselemente:
·
Das FS-Verhältnis der
6 hexagonalen Punkte zu den 3 hexagonalen Linien beträgt 96:32
= 32*(3:1), also 2:1 Elemente haben
das Vehältnis 3:1: Die Zahlen 3 und 4 bilden eine
Einheit.
·
Das FS-Verhältnis der
4 oberen zu den 6
unteren Erweiterungszahlen beträgt 63:70 = 7*(9:10).
Die Aufteilung von 4 Punkten und 6 Linien ergibt die FS
73+60 = 133. Die Einzelziffern von 73 bedeuten 7
hexagonale + 3 Erweiterungspunkte, 60 = 6*10 je 10
Punkte von jeder der 6 Ecken des
Tetraktyssterns aus.
·
Die FW der vier FS
sind:
|
|
Hexagon |
Erweiterg. |
sm |
||
|
|
P |
L |
P |
L |
|
|
FS
|
96 |
32 |
73 |
60 |
261 |
|
FW |
13 |
10 |
73 |
12 |
108 |
|
108 = 9*12; 261:108 = 9*(29:12) |
|||||
9*12 ist, als 3*(3+4) verstanden, auf je 3 Linien und 4 Punkte je Tetraktysseite beziehbar. 108 ist auch die FS der Zahlen 12-21 (s.u.).
Ein DR-Kreuz läßt sich zu einem Oktaeder zusammenfügen. Aus 29 Elementen besteht der Rahmen, der 12 Binnenelemente umschließt:
|
|
c)
13 bis 31 auf Punkten und in Dreiecken
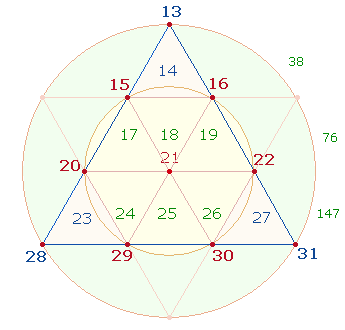
1. Die 19 Zahlen lassen sich ebenso auf 10 Punkten und in 9 Dreiecksflächen anordnen:
|
|
Diese Anordnung
ermöglicht ein ZS+FS-Verhältnis von 9
Zahlen auf den Punkten des Tetraktysrahmens und 10
Zahlen auf den 9 Dreiecksflächen und dem Mittelpunkt:
|
Z |
ZS |
FS |
sm |
|
9 |
204 |
132 |
336 |
|
10 |
214 |
129 |
343 |
|
|
418 |
261 |
679 |
|
336:343 = 7*(48:49) |
|||
|
132:129 = 3*(44:43) |
|||
Die ZS+FS der 4 Zahlen auf der rechten Tetraktysseite und die übrigen 5 Zahlen sind 82+65 = 147 und 122+67 = 189, ihr Verhältnis 21*(7:9).
Der Mittelpunkt bewirkt eine ungerade Gesamtzahl von symmetrischen Elementen und ist variabel in seiner Zuordnung. Die Mittelpunktszahl 21 enthält durch den FW 10 und der Summe 31 in den Einzelziffern die Zahlen 3 und 4 in sich.
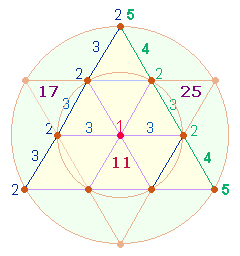
2. Die ZS+FS der 9 Dreiecksflächen ist 193+119 = 312 = 24*13, der 10 Punkte 225+142 = 367. Die Primzahl 193 gibt die Punktestruktur des Tetraktyssterns wieder:
|
|
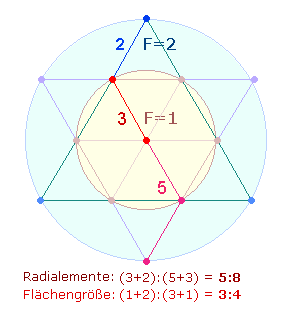
Die FW von 193 und 225 sind 193+16 = 209 und damit die Hälfte der Gesamt-ZS 418. Die Einzelziffern des Produkts 24*13 bezeichnen die Entsprechung von Radialelementen zum Kreisflächenverhältnis der beiden konzentrischen Kreise:
|
|
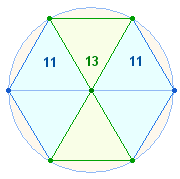
3. Drei Gruppen von Zahlen zeigen FS-Beziehungen: 6 hexagonale Flächen, 6 Erweiterungszahlen, 7 hexagonale Punkte: 78+96+87 = 261. Die ersten beiden FS bilden mit der dritten das Verhältnis 174:87 = 3*29*(3:1). Wiederum ist die Kombination von 2:1 und 3:1 erkennbar. 78 und 87 sind Umkehrzahlen für 6 Dreiecksflächen und 7 Punkte. Die Durchschnittszahl je hexagonaler Fläche ist 13.
1. Die Kreisflächenverhältnisse 1:2 und 1:3 sind wesentlich für das Verständnis des dreieinen Gottes. Deshalb lohnt eine Untersuchung, wie die Zahlen 12 bis 21 und 13 bis 31 miteinander korrespondieren.
Es wurde bereits erwähnt, daß die FS der Zahlen 12 bis 21 108 ist, sodaß sich das FS-Verhältnis 108:261 = 9*(12:29) ergibt:
|
ZW |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
165 |
|
FW |
7 |
13 |
9 |
8 |
8 |
17 |
8 |
19 |
9 |
10 |
108 |
|
sm |
19 |
26 |
23 |
23 |
24 |
34 |
26 |
38 |
29 |
31 |
273 |
|
|
|
156 = 12*13 = 6*26 |
|
|
|
|
|||||
|
165 = 5*33; 273 = 21*13 |
|||||||||||
In zweistelliger Zusammensetzung erscheinen die beiden trinitarischen Verhältnisse zweimal in den ZS+FS 156 und 273, wobei 12 sich in 21 umkehrt.
Nun sind die Zahlen 12-21 durch 13-31 umschlossen. Von der umschließenden FS 261 ist also 108 abzuziehen und das Differenzverhältnis beträgt 153:108 = 9*(17:12). Aus den Verhältniszahlen 17 und 12 bestehen die Rahmenelemente des hexagonalen und des Erweiterungsbereichs des DR-Kreuzes:
|
|
17:12 Elemente geben das Kreisflächenverhältnis 1:2 wieder.
2. Die ZS+FS der beiden Zahlenreihen beträgt 273+679 = 952 = 7*8*17. Nun ist die ZS konzentrischer Paare der Zahlen 12-21 und 13-31 jeweils 33 und 44, zusammen 77 und somit durch 7 teilbar. Auch die Gesamtsummen 273 und 679 sind durch 7 teilbar. Zu untersuchen sind konzentrische Zahlenpaare, deren ZS+FS durch 7 teilbar sind. Dabei ist zu beachten, daß die symmetrische Mitte einmal aus 22 und einmal aus 16+17 besteht. Die Untersuchung erfolgt von innen nach außen (9 obere + 10 untere Zahlen) und von außen nach innen (5+5 Zahlen):
|
|
1 |
2 |
3 |
4 |
5 |
|
5 |
4 |
3 |
2 |
1 |
2 |
3 |
4 |
5 |
|
5 |
4 |
3 |
2 |
1 |
|
|
|
ZF |
13 |
14 |
15 |
16 |
17 |
|
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
198 |
27 |
28 |
29 |
30 |
31 |
|
|
|
FW |
13 |
9 |
8 |
8 |
17 |
55 |
8 |
19 |
9 |
10 |
13 |
23 |
9 |
10 |
15 |
116 |
9 |
11 |
29 |
10 |
31 |
90 |
|
|
ZF |
|
44 |
|
44 |
44 |
|
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
165 |
75 |
|
44 |
|
44 |
|
|
FW |
|
19 |
|
19 |
26 |
64 |
7 |
13 |
9 |
8 |
8 |
17 |
8 |
19 |
9 |
10 |
108 |
|
|
37 |
|
44 |
81 |
|
|
|
63 |
|
63 |
70 |
196 |
62 |
34 |
36 |
55 |
41 |
43 |
92 |
363 |
|
|
81 |
|
88 |
169 |
|||
|
|
|
|
|
|
|
|
47 |
18 |
18 |
38 |
31 |
28 |
44 |
224 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
109 |
52 |
54 |
93 |
72 |
71 |
136 |
587 |
|
|
|
|
|
|
|||
Farblich sind zwei Hauptgruppen unterschieden: Grün unterlegte ZS+FS Summen (63,
63, 70) sind jeweils durch 7 teilbar,
weiß unterlegte ZS+FS sind
nicht durch 7 teilbar. Die ZS+FS von zwei
benachbarten, braun
unterlegten Zahlenpaaren (109+136) sind nur zusammen durch 7 teilbar.
Auf dem linken Flügel sind die durch 7 teilbaren (63), auf dem rechten Flügel die nicht durch 7 teilbaren (88) paarigen ZS+FS angeordnet. Die Umkehrsummen 196 und 169 sind die Quadrate von 14 und 13, die FS 64 und 81 als Quadrate von 8 und 9 lassen sich auf ein 9*9 Punkte-Quadrat mit 64 Einzelquadraten und auf den Faktor 17 der Gesamt-ZS+FS 952 beziehen.
Sowohl im Mittelbereich als auch auf den äußeren Flügeln sind die ZS+FS von jeweils 3 konzentrischen Zahlenpaaren durch 7 teilbar und 2 nicht durch 7 teilbar, und zwar jeweils an 2. und 4., 5. Stelle sowie an 1. und 3. Stelle. Die entsprechenden Gesamtsummen sind 567:385 = 7*(81:55). Die Anordnung der jeweils 3 und 2 Zahlenpaare entspricht den zweimal 3+2 Radialelementen einer DR-Zickzacklinie, des hexagonalen und des Erweiterungsbereichs:
|
|
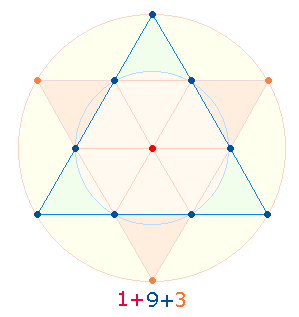
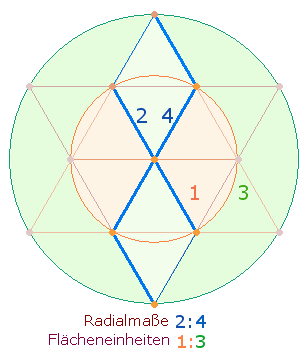
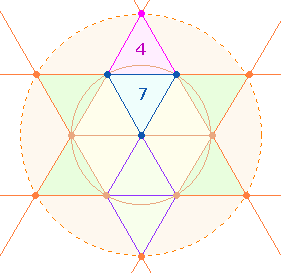
Die zwei zusammenhängenden Zahlenpaare 4 und 5 beziehen sich offensichtlich auf den Erweiterungsbereich des Tetraktyssterns und dem äußeren Kreisring, dessen Fläche das Doppelte der hexagonalen Kreisfläche beträgt:
|
|
Den Elementen 2 4 5 entsprechen 3 Kreisflächeneinheiten, den Elementen 1 3 1 Kreisflächeneinheit.
3. Daß die Innenpaare 5 und 4 zusammengehören, zeigt sich besonders in den FS der oberen und unteren Reihe: (8+15)+(19+10) = 52; (7+10)+(13+9) = 39; 52:39 = 13*(4:3). Für beide Reihen gibt es demnach das FS:ZS-Verhältnis 13:22 (52:88, 39:66). Die Einzelziffern des Verhältnis sind wiederum auf den hexagonalen und Erweiterungsbereich der DR-Zickzacklinie beziehbar: 1 Kreisflächeneinheit entsprechen 3 Radialelemente, 2 Kreisflächeneinheiten 2 Radialelmente.
Ebenfalls 13:22 ist das FW:ZW-Verhältnis der Symmetriemitte 22 der Zahlen 13-31. 2*11 ergibt die Gemeinsamkeit 13 als 35 Elemente dreier Hexagonfiguren:
|
|
Eine Rautenfigur aus 11 Elementen besteht aus 2 Flächen, 4 Punkten und 5 Linien und entspricht so den drei Zahlenpaaren, deren ZS+FS jeweils durch 7 teilbar ist, wie oben ermittelt wurde.
Es liegt nahe, den ZS+FS 7*35 der inneren Zahlenpaare den ZW+FW 35 der Mittelpunktszahl 22 hinzuzufügen. Es ergibt sich somit das ZS+FS-Verhältnis des Innen- zum Außenbereich 280:196 = 28*(7:10) = 476 und damit die Hälfte der Gesamt-ZS+FS 952. Die Verhältniszahlen 7 und 10 sind zweifach beziehbar: auf 7 hexagonale + 10 Tetraktyspunkte und 7 Punkte + 10 Linien der DR:
|
|
|
7:10 Punkten im Tetraktysstern entspricht das Kreisflächenverhältnis 1:3.
Fügt man den FW 13 der Mittelpunktszahl 22 der FS 64 der äußeren drei Zahlenpaare hinzu, ergibt sich das FS-Verhältnis 77:91 = 7*(11:13) = 7*24 = 168. 77 ist die FS der Zahlen 1-13, deren Summe 91 = 7*13 beträgt. Ebenso wie 7:10 Punkte geben auch 7:13 Punkte des Tetraktyssterns das Kreisflächenverhältnis 1:3 wieder.
Das ZS:FS-Verhältnis der ermittelten ZS+FS 476 ist 308:168 = 28*(11:6). Hier ist der Primfaktor 17 aufgeteilt in 11 Elemente der Raute und 6 zusätzliche Elemente, die zusammen eine stilisierte Fischgestalt haben und von den drei Eckpunkten der Tetraktys aus erkennbar sind:
|
|
4. Die erste Hälfte der Gesamt-ZS+FS 952 kam durch Auslassung des 2. Innenpaares zustande, aber mit Einschluß des ZW 22 und seines FW 13 unter der Innennummer 1. Die beiden anderen Mittelpunktszahlen 16+17 mit ihren FW gehören ebenfalls der Innennummer 1 an und fallen an die zweite Hälfte. Es ergeben sich somit für die beiden ZS+FS-Hälften die Numerierungssummen 21 und 10, zusammen 31. 10 ist der FW von 21.
Das ZS:FS-Verhältnis der zweiten Hälfte ist 275:201. Für die zweimal zwei Summen ergeben sich folgende FW:
|
ZS |
FW |
FS |
FW |
|
308 |
22 |
168 |
16 |
|
275 |
21 |
201 |
70 |
|
|
43 |
|
86 |
|
86=2*43 |
|||
Die Einzelziffern der beiden Summen sind auf je 4 Punkte + 3 Linien der drei Tetraktysseiten beziehbar:
|
|
Die ZW/FW-Verrechnung ergibt:
|
|
ZS |
FS |
sm |
FW |
sm |
FW |
||
|
|
308 |
275 |
168 |
201 |
952 |
30 |
|
|
|
FW |
22 |
21 |
16 |
70 |
129 |
46 |
|
|
|
sm |
1081 = 23*47 |
1081 |
76 |
1157 |
102 |
|||
|
FW |
|
|
|
|
70 |
23 |
93 |
34 |
|
1157 = 13*89; 136 = 8*17 |
136 |
|||||||
136 und 102 sind die ZS und FS der Zahlen 1-16, 34 die Differenz zwischen beiden. 16 setzt sich aus 7+9 zusammen, den Komplementärzahlen zu 3+1. Die Summe der Zahlen 1-3 und 1-4 betragen 6+10 = 16. 5:3 Radialelemente geben in zwei Richtungen jeweils das Kreisflächenverhältnis 3:1 wieder, ebenso die Aufteilung (1+3)+6 Punkte der Tetraktys:
|
|
Die Gesamt-ZS+FS 952 ist 7*136.
5. Ein Bezug zur Tetraktys ergibt sich auch aus den zweimal zwei Summen des Innen- und Außenbereichs:
|
|
ZS |
|
FS |
|
||
|
|
I |
A |
|
I |
A |
|
|
|
363 |
220 |
|
224 |
145 |
|
|
FW |
25 |
20 |
45 |
17 |
34 |
51 |
Numeriert man die Punkte mit 2 und die Linien mit 3, ergibt sich für jede einzelne Tetraktysseite die Summe 17, für alle drei Seiten zusammen 45. Wenn man den Erweiterungsbereich mit 4 und 5 weiternumeriert, ist die Numerierungssumme je Seite 25:
|
|
6. Die ZS+FS 587 des Innenbereichs ist eine Primzahl. Sie bezeichnet 5+8 Radialelemente, die 7 Kreisflächeneinheiten wiedergeben:
|
|
Die ZW/FW-Verrechnung der beiden ZS+FS ergibt:
|
|
I |
A |
sm |
FW |
sm |
FW |
|
ZS+FS |
587 |
365 |
952 |
30 |
|
|
|
FW |
587 |
78 |
665 |
31 |
665 = 35*19 |
|
|
1617 = 7*231 >FW 21 |
1617 |
61 |
1678 |
841 |
||
|
|
|
|
28 |
61 |
89 |
89 |
|
|
|
|
|
|
|
930 |
Die Zahlen 16 und 17 bilden die Mitte der Zahlen 12-21, 231 ist die Summe der Zahlen 1-21. Die konstitutiven Zusammensetzungen 9+7 und 9+8 sind als Komplementärzahlen zu den zwei Kreisflächenverhältnissen 1:3 und 1:2 zu verstehen. 7*231 beleuchtet einen Bedeutungsaspekt der Zahl 28. Die DR aus 21 Elementen enthält 4 Dreiecksflächen. Ein einzelnes Dreieck besteht jedoch aus 7 Elementen. So kommt der Doppelaspekt von 21 und 28 Elementen zustande.
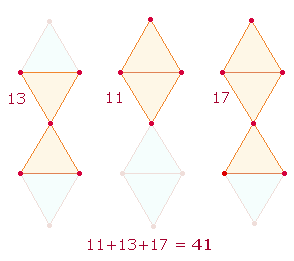
930 = 3*13*10 = FW 41 läßt sich auf 3+1+3 Punkte und 10 Linien der DR beziehen. Der FW 41 entspricht den Elementen von 3 geometrischen Figuren der DR:
|
|
7. Auffällig ist die zweimalige ZS+FS 63 des Außenbereichs, deren Summe 126 auch die des zweiten Innenpaares 72+54 ist. Die drei DR aus je 21 Elementen sind auf die Zusammenfügung zu Oktaedern hingeordnet. Damit jede DR sich mit jeder verbindet sind 6 DR erforderlich. Die Einzelziffern von 126 geben 9 Punkte des Tetraktysrahmens wieder. Das Verhältnis 72:54 = 18*(4:3) bedeutet 18 Elemente des Tetraktysrahmens und 4:3 Elemente je Einzelseite.
Die durch zweimal 126 zusammengefaßte ZS+FS und die übrigen Summen sind:
|
|
ZS |
FS |
||
|
|
252 |
700 |
87 |
282 |
|
FW |
17 |
21 |
32 |
52 |
Das ZS-Verhältnis 28*(9:25) weist auf zwei konzentrische Quadrate aus 9 und 25 Punkten als Entsprechung zu den beiden konzentrischen Tetraktyskreisen hin. Das Verhältnis von 3:4 Dreiecken wird durch die Fischfigur aus 17 und die ganze DR aus 21 Elementen dargestellt. Das Verhältnis 4*(8:13) gibt das Kreisflächenverhältnis 2:1 wieder:
|
|
8. Durch die Aufteilung der Gesamt-ZS+FS 952 in zwei Hälften geriet die anfängliche Einteilung in durch 7 und nicht durch 7 teilbare Zahlenpaare (ZP) in den Hintergrund. Dies ist noch nachzuholen:
|
|
außen |
innen |
|
|
|
||
|
|
ZS |
FS |
ZS |
FS |
GS |
GS |
GS |
|
13-31 |
88 |
81 |
66 |
31 |
154 |
112 |
266 |
|
12-21 |
|
|
66 |
53 |
66 |
53 |
119 |
|
|
|
|
132 |
84 |
220 |
165 |
385 |
|
266:119 = 7*(38:17); 385 = 35*11 |
|||||||
|
81:84
= 3*(27:28); 84:132 = 12*(7:11) = 12*18 = 216 |
|||||||
|
165:220 = 11*(15:20)
= 55*(3:4); 112:154 = 14*(8:11) |
|||||||
Die ZS+FS 266 und 119 der 13-31 und 12-21 Zahlenpaare sind jeweils durch 7 teilbar. Die Teilbarkeit durch 7 setzt sich fort im Aufteilungsverhältnis 3:4 der FS:ZS.
Die ZS+FS 216 des inneren Bereichs ist eine Umkehrung zu 126, der ZS+FS des 2. inneren Zahlenpaares:
|
ZP |
1+3 |
2 |
|
|
ZS |
132 |
77 |
209 |
|
FS |
84 |
49 |
133 |
|
sm |
216 |
126 |
342 |
|
133:209 = 19*(7:11); 342 = 19*18 |
|||
|
49:84 = 7*(7:12) = 7*19 |
|||
Beide Einzelergebnisse haben jeweils das FS:ZS-Verhältnis 7:11, das im Tetraktysstern die hexagonalen Elemente und die Gesamtzahl der Rautenelemente darstellt und das Kreisflächenverhältnis 1:3 wiedergibt:
|
|
Das Produkt 19*18 weist auf die 37 Elemente der Tetraktys hin: 10 Punkte + 9 Dreiecksflächen und 18 Linien hin, das Produkt 7*19 auf 7 Kreisflächeneinheiten von 19 DR-Elementen.
Zu dem ermittelten Ergebnis läßt sich noch die ZS+FS 126 der äußeren Nummern 2+4 hinzufügen:
|
ZP |
1+3 |
2 |
2+3 |
sm |
|
ZS |
132 |
77 |
88 |
297 |
|
FS |
84 |
49 |
38 |
171 |
|
sm |
216 |
126 |
126 |
468 |
|
171:297 = 9*(19:33) = 9*52 |
||||
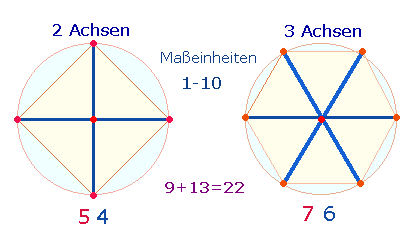
Die verbleibende Summe 484 ist das Quadrat von 22. Das FS:ZS-Verhältnis ist 22*(9:13). Die Verhältniszahlen bezeichnen die Elemente eines zwei- und dreiachsigen Achsenkreuzes:
|
|
12 Punkte begrenzen 10 für das Dezimalsystem relevante Maßeinheiten. 22*22, verstanden als 4*22, ist auf das Zustandekommen eines Oktaeders aus 4 Rauten beziehbar. Dem FW 26 von 484 entspricht die Zahl der Oktaederelemente. Die ZS 53*11 = FW 64 = 8² kann als Doppelaspekt von 26+27 Oktaederelementen gesehen werden, indem bei der zweiten Zählung das Volumen hinzugefügt wird. Die ZS 297 = 27*11 bezeichnet somit die zweite Zählung.
9. Das Verhältnis 7:11 wird ein weiteres Mal erreicht, wenn man zur ZS+FS 385 = 35*11 der 4 einzelnen nicht durch 7 teilbaren Zahlenpaare die inneren Nummernpaare 4+5 hinzufügt:
|
ZP |
4+5 |
8 |
sm |
|
ZS |
154 |
220 |
374 |
|
FS |
91 |
165 |
256 |
|
sm |
245 |
385 |
630 |
|
35*(7:11) = 630 |
|||
Ein FS:ZS-Verhältnis 7:11 wird möglich, wenn man die ZS+FS der äußeren Zahlenpaare 2+4 hinzufügt:
|
ZP |
17 |
6 |
sm |
|
ZS |
374 |
88 |
462 |
|
FS |
256 |
38 |
294 |
|
sm |
630 |
126 |
756 |
|
294:462 = 42*(7:11) |
|||
Schließlich hat das innere Zahlenpaar 2 allein durch 49:77 das FS:ZS-Verhältnis 7:11, sodaß nun das Gesamtverhältnis lautet 343:539 = 49*(7:11) = 882. Die FS 343 weist durch 3*(4+3) auf die Punkte und Linien der drei Tetraktysseiten hin. Der gemeinsame Teiler 42 faßt die Numerierungssummen 17+25 je Seite zusammen. Die drei durch 3 geteilten Gesamtsummen sind 6+15+20 = 41. Es ergibt sich so der Doppelaspekt von 49+41 = 90 je einzelne Tetraktysseite und 270 als Gesamtsumme, zusammengesetzt aus 21+18 = 39, 51+45 = 96 und 75+60 = 135. Die Gesamt-FS 369 = 9*41 enthält die Aspekte 41 und 9.
Übrig bleibt das äußere Zahlenpaar 5 mit der ZS+FS 44+26 = 70: 882+70 = 952, es hat seine besondere Bedeutung durch das FS:ZS-Verhältnis 2*(13:22). Dieses äußere Zahlenpaar 5 und die inneren Zahlenpaare 5+4 ergeben zusammen das FS:ZS-Verhältnis 117:198 = 9*(13:22), mit 22+13 des Mittelpunktes ist das Endverhältnis 10*(13:22) = 350.
Eingestellt: 30. Oktober 2018